如何在 DeFi 世界通过交易策略获得收益？

讨论了那么多去中心化金融（DeFi）的发展趋势和对我们所处的世界的影响，你是否考虑过如何在目前的 DeFi 生态中获利？专业的数字资产理财平台 Amber Group 提出了去中心化流动性策略（Decentralized Liquidity Strategies），指出在 DeFi 体系通过交易策略获利的方法和途径。

撰文：Amber Group 来源：链闻 ChainNews

在去中心化金融（DeFi）体系内，有多种通过交易策略获得收益的方法。基本策略可分为两大类：

• 为依赖于第三方流动性的应用提供链上有保证的流动性；
• 在已有链上流动性的应用里抽取费用。

Keeper 策略

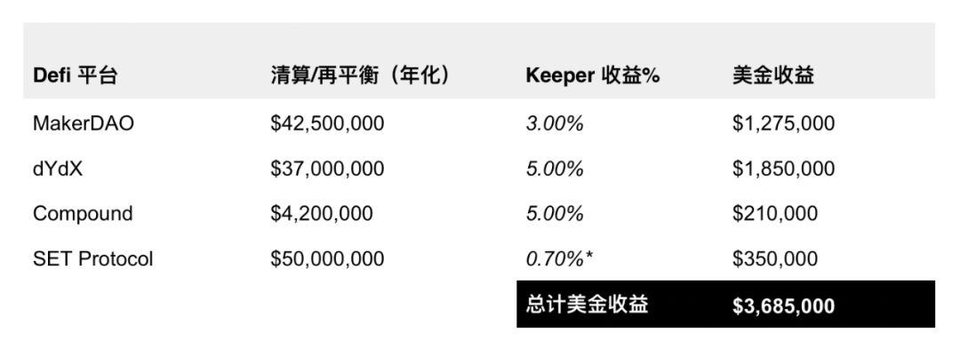
目前， 在去中心化金融市场里有几种方式可以赚取比「无风险」利率更高的回报 。此处我们所言的「无风险」利率可以看成是 Compound Protocol 上的贷款利率，或者是即将推行的 DAI 存款利率 (DAI savings rate, DSR) 。除了投机交易之外，市场参与者还可以通过充当「 keeper 」的角色获得风险溢价。

Keepers 独立于各个去中心化金融平台，通过利用在 MakerDAO、dYdX、SET Protocol、DDEX 和 Compound Protocol 等应用里的获利机会，来维持各种系统中的市场平衡。在这些去中心化应用里，外部参与者可以通过执行以下承销或提供流动性的功能，获得经济收益：

• 在 MakerDAO 上清算有爆仓风险的抵押债仓 （Collateralized Debt Position, CDP） ：参与者可以调用 bite 函数来承担所有债务以换取 PETH (Pooled ETH) 抵押品和 3% 的清算费。
• 在 dYdX 上调用 liquidate() 函数清算并接管抵押不足 （小于 115%） 的头寸， 并收取 5% 的清算费。
• 在 Compound Protocol 上调用 liquidateBorrow() 函数清算并接管抵押不足 （小于 150%） 的头寸，并收取 5% 的清算费。
• 在 DDEX 上调用 liquidateAccount() 函数清算并接管抵押不足 （小于 110%） 的头寸：抵押品在减价式拍卖后，参与者可以收取任何超出维持保证金盈余的 5％的费用。
• 在 SET Protocol 上，参与者可以通过竞标在 Set 组合再平衡拍卖期间竞争利润，以及发行和赎回被低估 / 高估的 Sets。

根据目前在上述应用中可用的有关清算和再平衡的年化数据，我们可以估算出 Keepers 一年累计的利润 （假设市场无摩擦且没有对冲成本） ：

*这里假设 Set Protocol 上的做市商利润相当于减价拍卖过程中的交易滑点（再平衡买价 / 卖价 vs 市场卖价 / 买价），而 0.7% 是 Set 再平衡时减价拍卖的平均滑点。

总的来说，我们可以估计， 在目前的市场状态下，Keepers 的年收益在 300～400 万美金之间 。这里忽略了 Maker 上 PETH 持有者在清算时能获得的罚金，因为多抵押 DAI （multi-collateral DAI, or MCD） 的清算罚款最终将归 MKR 持有者所有。由于估算套利利润较为困难 , 我们同时也排除了利用 DAI / ETH，DAI / WETH 和 PETH / WETH 之间定价错误套利的 Maker Keepers。

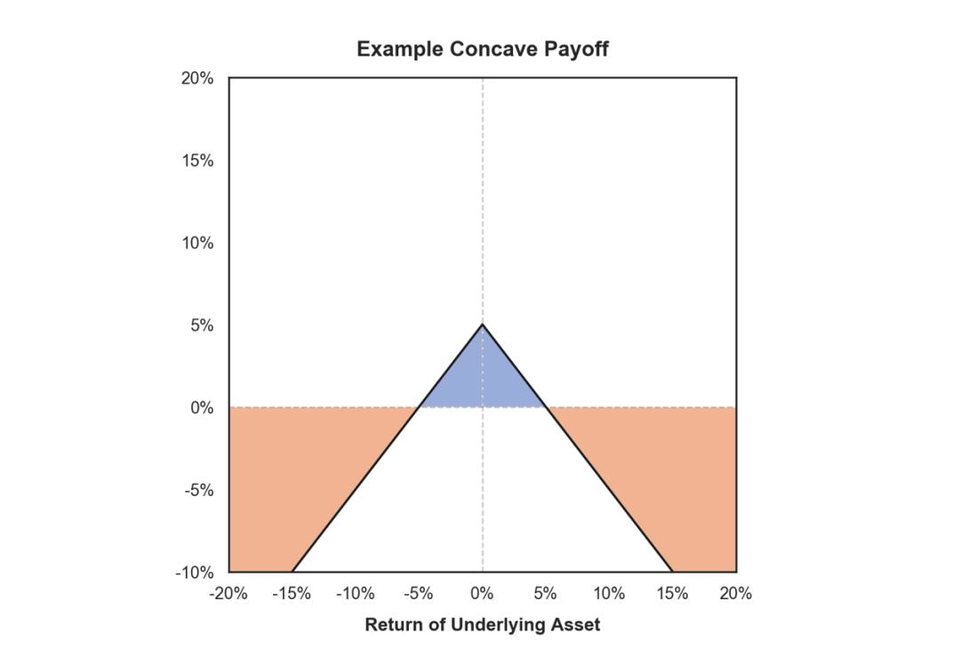
理论上来说，Keeper 策略 （除了 Set 拍卖以外） 的敞口可以通过一串连续的敲入期权合成复制。对于单个给定的期间，我们可以通过建立标的抵押资产价格的过程，并定义其最大和最小值，来描述 Keeper 策略的收益结构：

𝑆 = 𝑆𝑡 , 0 < 𝑡 < 𝑇 as 𝑚𝑆 = inf 𝑆𝑡 ; 0 < 𝑡 < 𝑇 and 𝑀𝑆 = sup 𝑆𝑡 ; 0 < 𝑡 < 𝑇 .

这里敲入期权的障碍价格 L （清算门槛 %） 设于即期价格 S0 （抵押率 %） 之下， 即 L < 𝑆0。在它的有效期内，S （抵押率 %） 必须至少有一次跌到了障碍价格之下，该期权才会生效，并成为普通实值看涨期权：

Φ𝐷𝐼 𝑆𝑇, 𝑚𝑆 = 𝑆𝑇 − 𝐾 +𝟏(𝑚𝑆 ≤ L)

再来看 Set Protocol ，拍卖参与者使用 TokenSets 的长期预期收益结构高度依赖于各种代币组合策略之间的相关系数。但从广义上讲，我们可以将 Keeper 策略的敞口视为做多波动率。

Uniswap 上的自动做市机制

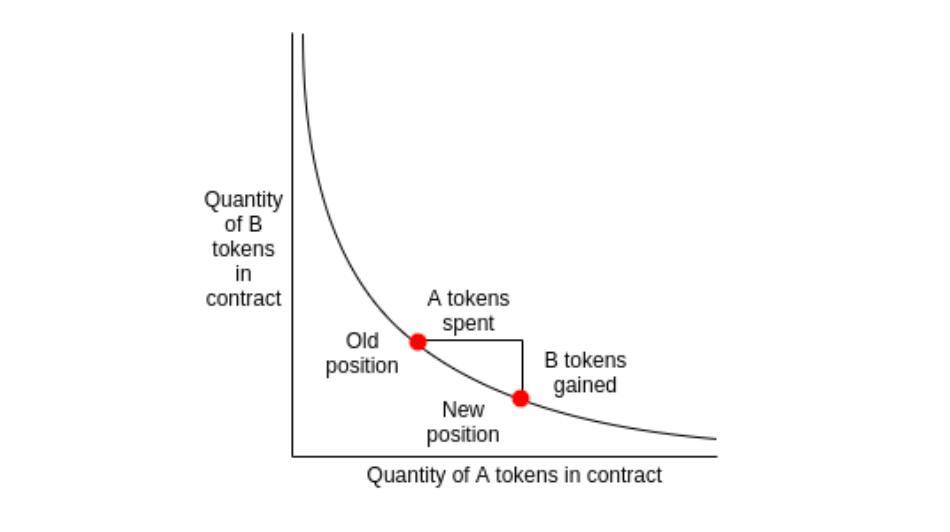
Uniswap 的自动做市机制建立在恒定乘积定价的模型之上 —— ERC20 代币对的汇率计算基于公式 x * y = k，其中 x 和 y 是流动性池中的代币数量 （比如 ETH 和 DAI） ，而 k 是恒定乘积。

代币的汇率始终落在联合曲线上的特定点上，因此两个流动性池的乘积在交易前后始终保持不变。例如 : x = ETH，y = DAI，x * y = k，y / x = p，受价者在每笔交易中支付 0.3％的费用，该费用将被加回到流动资金池中。

流动性提供者 （Liquidity Providers, LPs） 为资金池提供代币，并获得代表其在池中份额的代币 （LP shares) 作为回报。根据恒定乘积定价，任何方向 （即任何交易活动） 的价格变化都会对 LP 产生负面影响。这意味着某一 Uniswap LP share 的收益与从流动性增加到流动性撤除之间的资产相对价差，以及资金池累计的交易费用相关。换句话说，当最终价格与 LPs 最初提供流动性时的价格一致时，LPs 可以获得最高的利润。

来源： https://github.com/MFFouda/Research/blob/master/Uniswapanalysis.m

Short Straddle Payoff

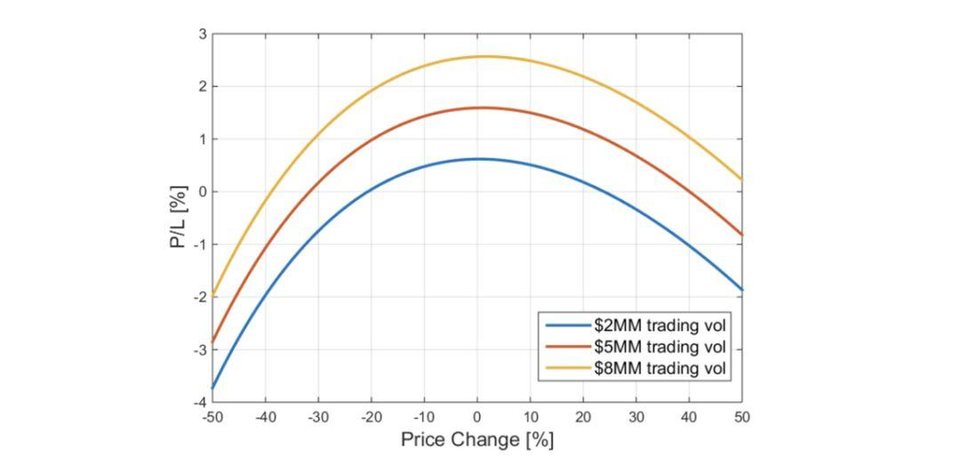
如此，假设：

• 资金池总量保持不变 （即没有增加或提现）；
• 代币价格遵循随机过程；
• 资金池累计的交易费用归 LPs 所有。

我们可以带有启发性的把 Uniswap LPs 的收益函数想象成卖空永续实值跨式期权，其执行价格会根据交易量对流动性的比例 （volume per unit of liquidity） 不断地重新调整。

更实际的来说，这个收益结构可以通过卖空一串连续到期的相同执行价格的短期跨式期权来估算。即，在 t+0 （进入资金池） 时，卖出实值跨式期权，然后在 t+1, t+2...t+每个时间段递归卖出同样执行价格的跨式期权 （例如每隔一个区块） 。如此，该收益应是因代币价格变化造成的暂时损失与累计的溢价 （池中交易费用） 之和的函数。

利用衍生品来复制并估算各种 DeFi 策略的收益意味着，对于给定的一组参数，市场参与者将能够直接推断流动性资金池中的代币对的波动率，以及 Keeper 策略的必要收益率等等 （至 少抽象的来说） 。这同样也可以成为在去中心化金融原生的环境里关于投资组合的构建和优化方面有趣的思想实验。

本文撰文机构 Amber Group 是服务全球机构及高净值客户的一站式数字货币交易理财平台，提供专业完整的机构级场外、大宗、资管、流动性及衍生品服务。